CHAPTER 3: History to 1800

3.5 The Baroque, Rococo and Classical Periods 1600-1800

3.5.1 The west

1.2. Higher cultures in the 17th & 18th centuries: Romance language-area

Instruments: Characteristics of 17th & 18thC. salterii and psaltérions

[153c]

Bridging

Having considered general points and the body of the instrument, we pass to the feature which contains the essential character of any dulcimer, the bridging.

In cases where the bridges are intact, there is no problem; but when they are missing it may nevertheless be possible to reconstruct them from an examination of the wrest-pins, since the period at which a pattern repeats itself will indicate how many bridges there were, while a change in the pattern indicates the beginning or end of a bridge.

To take a simple example: if an instrument had three treble courses, each with two strings, interspersed by two bass courses each with a single string, the wrest pins would appear thus: in figures "2 1 2 1 2"; if we link similar numbers viz. , we see that the pattern repeats itself after two figures, and there were two bridges.

Imagine an instrument with three bridges, each having three courses, of three, two and one string respectively; the bridging would appear as shown in fig. 93,

fig. 93: triple bridging

and the wrest-pins would appear thus or in figures

Thus, the pattern repeats itself every three figures, and there were three bridges. If one bridge stopped short while another carried on, and if the spacing of the courses over each bridge were consistent - as is almost always the case - then there would be a gap in the wrestpins: imagine a treble bridge of six double courses, the first four of which were interspersed with three single bass courses, as in fig. 94.

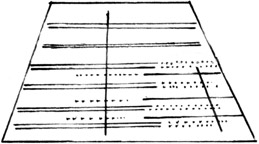
fig.94 - 6 ^II + 3 ^I

The wrest-pins would then appear thus:

If an instrument without bridges has such a pattern of pins, we may deduce the bridging by reversing the reasoning. What cannot be gauged simply from the wrest-pins is the positions of the various bridges; when there are two bridges, a single treble and a single bass bridge, the treble is virtually always placed at 2:3 fron the left, and the bass at the right-hand edge (and this may be verified by checking for the position of any support bridges inside the soundbox): but a third bridge is not always so easy to locate. Most instruments with a short third bridge follow the layout suggested by Mersenne, i.e. a little 'foot' bridge in the left-hand corner nearest the player; but the other instruments have a longer second bass bridge behind the first - as shown in the Battaglia tuning diagram:

click!

- on the right hand side giving extra chromatic notes within the same range. A similar wrest-pin arrangement might also indicate a left-hand bass bridge extending the compass downwards, but without the chromatic potential.

An instrument having no variation in the number of wrest-pins is likely to have been furnished with two single long bridges of equal length, but this is not the only possibility. Other complications to be allowed for are a maker drilling more holes than he later furnished with pins, and a player not stringing every pin.

click! fig. 92: Stockholm, Roca 1734

The pins are arranged in figures, thus:

6666666657676767676767676767-7

The part of the scheme which forms a repeating pattern is identified:

The courses with the higher number of strings are assumed, from experience, to be the higher pitches, i.e. the treble courses, and are entered on a plan of the instrument.

This leaves the following:

On the assumption that the first bass courses continue, evenly spaced, for the length of the instrument, the eevenly-spaced '6s' are extracted, and entered on the plan:

the remainder is thus four evenly-spaced '6s':

-6-6-6-6--------------------

Since the bass bridge starts lower than the treble, there are four right-hand bass-notes before the treble bridge begins (not 3, as 13 minus 10 would lead one to suppose) and these might well correspond to the four '6s' remaining: it therefore seems likely that these latter should be on the left, extending the compass downwards in step alternately with the bottom four notes of the right-hand bass bridge, viz:

What we cannot tell from the pins is whether or not the bridges were whole or divided, or even chessmen; if there are any bridge portions remaining at all, or even stains on the soundboard, this may be deduced, of course.

In the second example, the problem is not to see where the bridges lie, for the Museum Curator has already positioned them, but to tell how many strings each of the courses has, for the photograph does not show this clearly (fig. 98):

Here the numerical pattern is: which clearly repeats at the third digit; the odd '3' towards the end marked * may be considered a '4' since there is a hole there for a fourth pin: how it came to be missing or omitted is another question. Extracting the '5s' gives a treble bridge of 11^V:

and leaves:

from which we may take the '4s' occuring at every third position starting from the upper end (right); this we may take to be a bass bridge of 9^IV, starting three notes lower than the treble:

and leaving: -44--4--4--4--4 --------------------

These imply another, shorter, bridge, of 4^IV and a single bridge, 1^IV; this time, the treble bridge does not end four notes from the player, so these four courses may not be a lower extension of the range; the treble bridge in fact ends one course before the player, so the single bridge should be placed on the left, leaving the 4^IV bridge as a chromatic second bass bridge, behind the first, and confirming the overall plan reconstructed by the Museum curator.

So much for the method of determining bridging in incomplete cases; next we should consider the various bridging types and it may be helpful to recall those identified up to this point.

It will simplify matters a little if, having noted that all examples in the period under review are trapezoid, we omit the digit from the class number which shows that, for the present at least: it would need to be replaced for any comparison with another period, of course.

We have so far introduced the concept of a digit to indicate the number of treble bridges, followed by another digit - if need be, separated by a comma - to show how many bass bridges there are; then the notion of chessmen bridges joined up by a wire was indicated by 'x' and chessmen bridges not so joined up (but still in a straight line) was given 'y': a single 'x' or 'y' signifies a row of little bridges corresponding to a single long bridge. We noted in passing that one example of a popular instrument from this period had a single long bridge divided into two parts, and since there is a great variety of such divisions among the upper-class instruments of the 17th and 18th centuries, we need to expand the range of symbols again. We will do this simply by showing the unity of the single bridge ('1') divided into as many parts as is the bridge it represents, 1. Thus if a long bridge is divided into two parts, we will show it by 1/2; if it is in three parts, by 1/3; note that the normal meaning of these fractions is 'one divided by two', 'one divided by three', but that we are using them here to mean instead 'one divided into two parts', 'one divided into three parts'. To be literal we should write 1/3+1/3+1/3 but this is too complex, especially with the more elaborate instruments.

There are examples of instruments with whole single bridges, divided single bridges, linked chessmen and separate chessmen; and these groups may occur on an instrument with two, three, four or occasionally even five bridges. Thus there are theoretically a dozen major types of bridging, of which eleven actually do occur; and since the treble bridge may be broken into up to five sections, and the bass bridge divided into up to three, the number of possible permutations is (11 x 5 x 3) = 165. It is perhaps not surprising, then, that there are only two or three examples of each kind, and that only two kinds - the two simplest- show any general currency.

Summary:

If we take the totals for the main groups, we see that 18 examples had whole bridges, 15 divided bridges, while of chessmen whether joined or separate there were only 5 (13%); so far as number of bridges is concerned, 12 had two bridges, 10 had three, and only three had four or five. Thus it seems that there was a hard core of instruments having simply two long bridges, but that there was also a rather large minority using either divided long bridges (of whatever number) or three bridges (of whatever type), to obtain extra range or chromatic potential.

The Berlin instrument, 2148, is interesting because it has a particularly high saddle, built rather like a low solid bridge: see Baines 1966.

All instruments use the ratio of 2:3 across the treble bridge, except the illustrations of Diderot and of Mersenne.